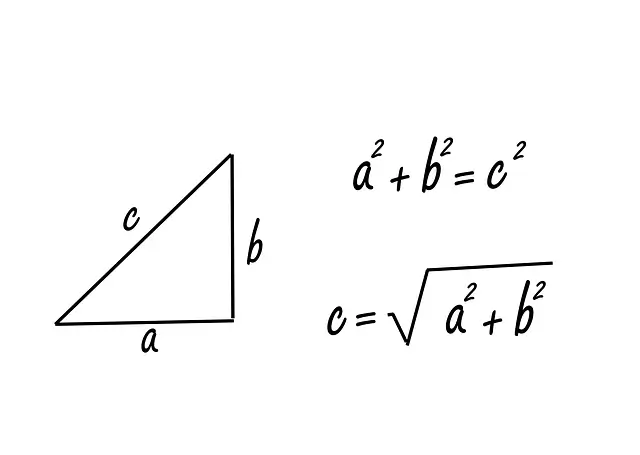Pythagore : Utilisation du théorème dans la construction

Sommaire

• Le théorème de Pythagore, expliqué simplement

• À quoi sert Pythagore en construction bois ?

• L’usage sur chantier : comment vérifier l’équerrage ?

• Tracer un angle droit avec la règle 3-4-5

• Conclusion : implantation d’un carport, d’un abri, d’une terrasse ou autre projet de construction

Pythagore ou le fameux theoreme qui a sans doute laisser pantois de nombreuses personne pendant les cours du collège. Pourtant ce théoreme est relativement simple a mettre en pratique et véritablement pratique dans la vie d'un charpentier ou toute personne désireuses de tracer un angle droit pour implanter un projet.

Le théorème de Pythagore s’applique uniquement dans un triangle rectangle (un triangle avec un angle à 90°).

Formule :
a² + b² = c²

• c est l’hypoténuse : le côté le plus long, celui qui est “en face” de l’angle droit.

• a et b sont les deux côtés perpendiculaires.

Sur un chantier : dès qu’une diagonale apparaît, Pythagore permet :

• soit de vérifier qu’un angle est bien droit,

• soit de calculer une longueur manquante .

Pythagore expliqué simplement

À quoi sert Pythagore en construction bois ?

Dans un projet bois, de nombreuses opérations supposent une géométrie correcte dès le départ :

• implantation d’un carport, d’un abri, d’une serre, d’une cabane, d’une terrasse ou d’une extension ;

• mise d’équerre d’un cadre de plancher (solivage, poutres de rive, muralière) ;

• contrôle d’un mur en ossature bois avant contreventement ;

• vérification de longueurs en charpente (chevrons, arbalétriers) ;

• positionnement de cloisons ou de murs sur le chantier.

L’objectif est d’obtenir une base saine, qui permette d’assembler et de construire sans contrainte. Le théorème de Pythagore est particulièrement efficace, car il s’adapte à pratiquement toutes les situations de chantier et à toutes les longueurs.
Dans la plupart des cas, cette méthode est plus fiable et plus précise pour implanter un bâtiment qu’une simple équerre posée dans un angle, souvent insuffisante sur de grandes dimensions.

L’usage sur chantier : comment vérifier l’équerrage ?

Méthode 1 (la plus rapide) : contrôler l’équerrage par les diagonales

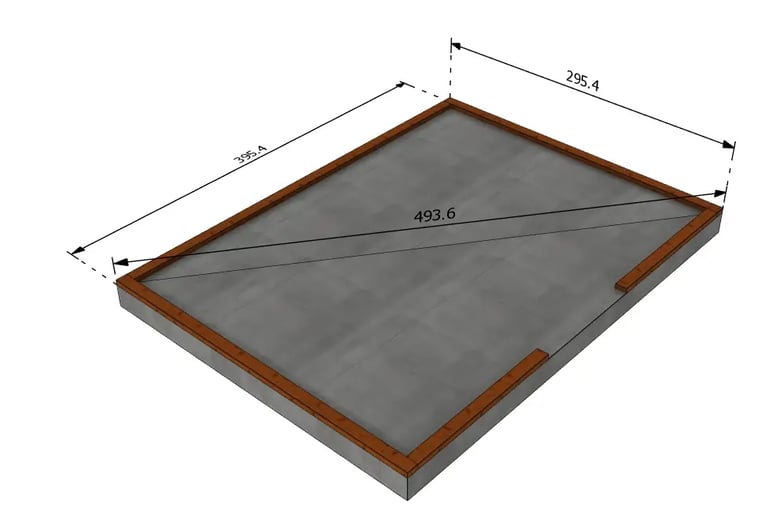
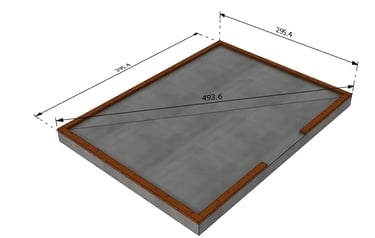
Cette méthode s’applique lorsque la forme à contrôler est un rectangle ou un carré. Le principe est simple : les deux diagonales doivent être identiques.
C’est l’approche la plus rapide quand les quatre côtés sont déjà tracés (ou déjà positionnés).

L’intérêt du contrôle par diagonales est qu’il permet de ne pas dépendre d’un support imparfait. Sur chantier, il est fréquent que la référence disponible ne soit pas parfaitement droite : bord de dalle, mur en béton, rive de coffrage, etc.
Dans ce contexte, se baser à l’équerre sur un bord douteux peut créer une erreur dès le départ, voire conduire à une mesure impossible (cote qui tombe dans le vide).

Bonne pratique : si la référence en place n’est pas fiable, il est préférable de créer un trait de référence propre, quitte à se décaler, puis de tracer une parallèle à ce trait.

Cas d’usage typiques :

• Vérifier l’équerrage d’une dalle béton ou d’un plancher bois 

• Implanter une construction (carport, abri, extension, terrasse…) 

• Mettre d’équerre un cadre de plancher / solivage (dont trémie d’escalier) 

• Contrôler un mur en ossature bois avant pose du contreventement (OSB) 

• Contrôler un cadre de terrasse avant platelage.

Procédure pas à pas :

1. Tracer ou positionner les éléments sur le chantier. Fixer provisoirement (ou marquer) de façon à pouvoir ajuster.

2. Mesurer la première diagonale : d’un angle à l’angle opposé, avec des repères nets (trait, vis, pointe).

3. Mesurer la seconde diagonale sur l’autre paire d’angles.

4. Ajuster si une diagonale est plus grande : fermer légèrement le rectangle du côté correspondant jusqu’à obtenir la même valeur.

5. Bloquer une fois l’égalité obtenue : contreventer / visser / ancrer, puis valider l’implantation (axes, appuis, poteaux, murs…).

Conseil pratique : sur des dimensions importantes, une différence de diagonales même faible se répercute vite au montage. Le contrôle des diagonales fait gagner un temps considérable ensuite.

En fonction du type de construction et du projet, il est toutefois possible de tolérer un léger jeu ou une petite différence, sans que cela ne pénalise l’ensemble. Il est difficile d’estimer précisément ce qui est acceptable ou non, car chaque projet est différent : il est donc important d’identifier où l’erreur va se répercuter et quel sera son impact.

Cela étant, à titre de repères, voici les ordres de grandeur que je considère généralement acceptables sur chantier. Ce sont des valeurs issues de la pratique : elles n’ont jamais compromis la qualité d’une implantation ou d’un montage, à condition de vérifier où l’erreur se répercute :

• ± 3 mm : équerrage d’un mur ossature bois ;

• ± 5 mm : équerrage d’un plancher ;

• ± 5 mm : implantation générale d’un projet ;

• ± 2 mm : réservation / ouverture dans un mur (fenêtre, par exemple).

Tracer un angle droit avec la règle 3-4-5

La règle 3-4-5 : qu'est ce que c'est ?

La règle 3-4-5, vous en avez peut-être déjà entendu parler par un proche, sans jamais oser demander ce que c’était.
Très utile à connaître, et tout aussi simple à appliquer sur le chantier, cette règle correspond tout simplement à l’application du théorème de Pythagore à un triangle rectangle dont les côtés mesurent 3, 4 et 5.

Il est indispensable que les trois mesures soient exprimées dans la même unité. Il est donc impossible de mélanger mètres et centimètres (pour des raisons évidentes de cohérence)

Si l’on applique le théorème, on obtient :

• 3² + 4² = 5²

• donc 9 + 16 = 25

• et 25 = 25

Un triangle dont les côtés mesurent exactement 3 – 4 – 5 est donc bien un triangle rectangle : il possède un angle droit. On comprend alors immédiatement l’intérêt sur le terrain : avec cette règle en tête, il devient possible de vérifier et d’implanter un angle droit très facilement.

Mais comment appliquer le 3-4-5 si les dimensions ne correspondent pas ?

C’est justement l’intérêt de la méthode : on n’est pas obligé d’utiliser 3 m, 4 m et 5 m. Il suffit de travailler avec des proportions équivalentes. Par exemple, si une dimension disponible sur le chantier est de 2,84 m, il est évident que l’on ne va pas pousser les murs pour obtenir 3 m.
Dans ce cas, on peut considérer que 2,84 m correspond à 3 unités. On cherche alors les valeurs équivalentes pour 4 et 5 unités.

On obtient :

Si 2.84 m = 3 unités alors pour :

• 4 unités = 2,84 × 4 / 3 = 3,786 m

• 5 unités = 2,84 × 5 / 3 = 4,733 m

Comment obtenir ces résultats ?

Grâce à un calcul de proportion (produit en croix), facile à faire avec une calculatrice. Bien qu'en pratique, la plupart des téléphones disposent aujourd’hui d’une calculatrice suffisante sur chantier avec la fonction √ (racine carré).
Et si l’on dispose plutôt d’une autre valeur (par exemple la longueur de 4 unités), il est également possible de retrouver la valeur de 5 unités :

Si 3.786 m = 4 unités alors pour :

• 5 unités = 3,786 × 5 / 4 = 4,733

Et si aucun moyen de calcul n’est disponible ?

Si l’on ne dispose d’aucun outil de calcul sur chantier, ou si le calcul mental devient trop contraignant, il est aussi possible d’utiliser des multiples simples, proches des dimensions du projet.
Sur chantier, il est préférable d’utiliser des valeurs plus grandes, car la précision est meilleure. Exemples de triplets pratiques :

• 0,60 – 0,80 – 1,00 m

• 1,20 – 1,60 – 2,00 m

• 1,50 – 2,00 – 2,50 m

• 1,80 – 2,40 – 3,00 m

• 3,00 – 4,00 – 5,00 m

• 6,00 – 8,00 – 10,00 m

• etc...

Plus le triangle est grand, plus l’erreur relative est faible, ce qui rend l’implantation plus fiable.

Exemples d’application du théorème de Pythagore sur des projets de construction :

Implantation d'une ossature bois sur dalle béton

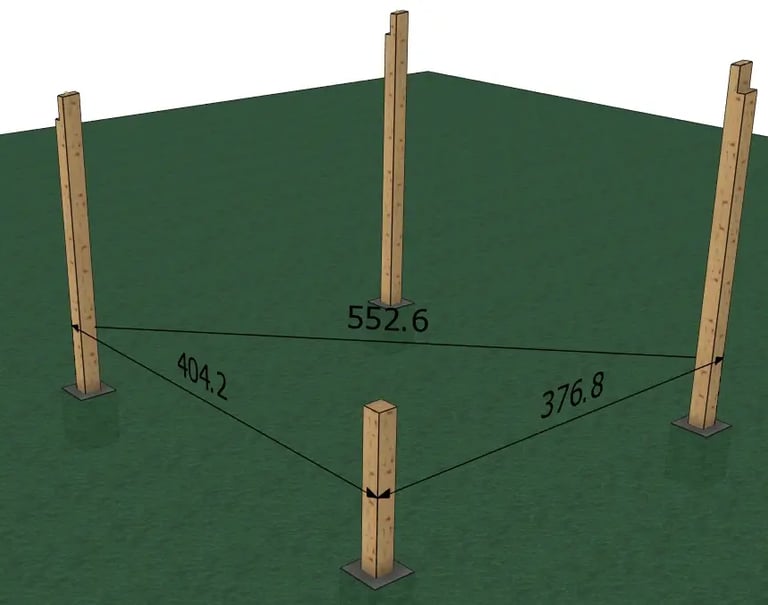
Implantation de poteau en bois sur plot béton

Dans le cas d’une implantation sur dalle (bois ou béton), il peut être suffisamment précis d’utiliser un multiple de la règle 3-4-5 pour vérifier l’équerrage d’une paroi. Il est recommandé de privilégier le plus grand multiple possible, afin d’améliorer la précision.

Dans le cas d’une implantation de poteaux sur des plots béton, lorsque l’environnement en périphérie empêche de tracer une ligne droite (herbe, cailloux, terre, etc.), il est préférable de repérer et tracer avec précision l’emplacement de chaque poteau ainsi que son équerrage, en respectant les dimensions indiquées sur le plan de construction.

Conclusion :  implantation d’un carport, d’un abri, d’une terrasse ou autre projet de construction

L’implantation d’une structure extérieure exige précision et rigueur. Qu’il s’agisse d’un abri de jardin, d’un carport ou d’une terrasse, le théorème de Pythagore permet de vérifier qu’un angle est bien à 90° et que l’ensemble est correctement d’équerre. Cela évite les désalignements qui finissent par compliquer le montage et peuvent entraîner des reprises coûteuses.

Lors de la réalisation d’un abri, le traçage d’un angle droit est une étape essentielle : si la base n’est pas parfaitement d’équerre, les assemblages forcent, les diagonales ne correspondent plus, et les éléments de finition deviennent plus difficiles à ajuster. En pratique, un simple mètre ruban et l’application du théorème de Pythagore (ou de la règle 3-4-5) suffisent pour contrôler l’équerrage dès le départ. La construction sera ainsi plus simple à monter, plus propre visuellement, et plus durable.